Receptor binding techniques: saturation (equilibrium) analysis
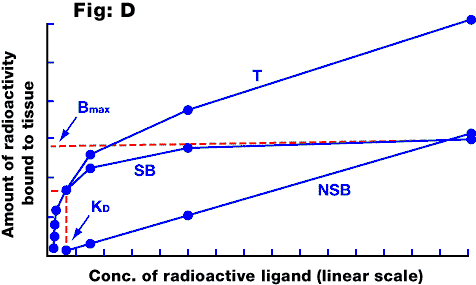
Fig D: Saturation curve for a ligand binding to a homogeneous receptor population. The total binding (T) includes a component of non-specific binding (NSB), which is non-saturable, and the remainder is specific binding (SB) which saturates at Bmax. Note that if the x-axis were logarithmic, the SB curve would be sigmoidal (compare with the log-concentration - response curve). The KD of the ligand is the concentration which occupies 50% of the receptors, and can be calculated from a Scatchard plot.
Scatchard analysis
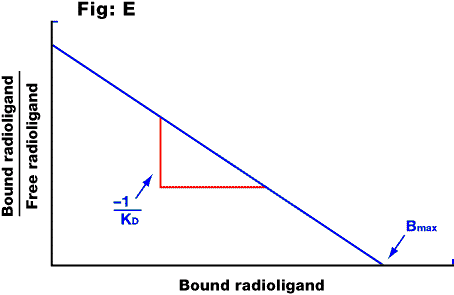
Fig. E: Scatchard plot of the saturable component of the data in the previous figure. The intercept on the x axis is equal to the Bmax; the slope is equal to -1/KD.
Scatchard analysis was, until recently, the standard method for analysing the equilibrium binding parameters of a radiolabelled drug with its receptor. The Scatchard plot is a graph of (on the y axis) the amount of radioligand bound divided by the amount of radioligand free in the solution, versus (on the x axis) the amount of radioligand bound. The Bmax and KD values are calculated as shown in the Scatchard plot above. This method is only valid where the drug binds to a single receptor population. If it binds to more than one type of site, the result will be a curved Scatchard plot (which could also occur where there is cooperativity in the binding, or various experimental artefacts). This method of analysis suffers from various statistical drawbacks and has now been superseded by computer-modelling to fit the data to one or more binding sites (see direct fit).
Other definitions:
Bmax
The maximum amount of drug (usually expressed in picomoles per mg protein) which can bind
specifically to the receptors in a membrane preparation. If one drug molecule binds to
each receptor, it also indicates the concentration of receptors in the tissue.
Direct fit
Computer-fitting of binding data (either saturation or competition data) to the logistic
equation:
Bmax [L]n
b = -------------
[L]n + Kn
where b = concentration of ligand bound to the receptor, [L] = conc. of free ligand, K is the dissociation constant for the ligand and n is a constant which should equal 1 if the assumptions in kinetics of binding are valid (it can represent the number of ligand molecules which bind to each receptor). When saturation or competition data are directly fitted to a logistic equation in this way, the Hill plot becomes unnecessary, since the calculated value of n is equivalent to the slope of the Hill plot.
Hill analysis
A method for analysing saturation or competition curves to determine whether the
interaction between the ligand and the receptor is competitive. As with the Scatchard
plot, the Hill plot has now largely been superseded by computer- fitting of the curves to
a one- or multi-site model. The slope of the Hill plot (sometimes called the Hill
coefficient or nH) should equal 1 if the ligand binds competitively and
reversibly. Slopes significantly greater than 1 may indicate positive cooperativity in the
binding; slopes less than 1 may indicate heterogeneity of binding sites or negative
cooperativity. However, there are also many artefactual reasons why the slope can differ
from the theoretical value.
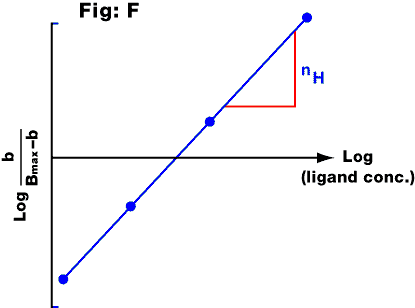
Fig. F: Hill plot from the saturation curve for a radioligand. The y axis
represents the log of the proportion of receptors occupied by radioligand divided by the
proportion not occupied (b = the amount of ligand bound, assuming that the NSB has been
subtracted; Bmax = the maximal amount of specifically bound ligand). The
significance of the slope (nH) is explained in the text.
KD
The dissociation constant for a radiolabelled drug determined by saturation analysis. The
units are moles per litre, and it is the concentration of drug which, at equilibrium,
occupies 50% of the receptors. Its reciprocal is called the affinity constant, sometimes
abbreviated to Kaff. (See kinetics of binding).
k1 or k+1
The rate constant for association of a drug with its receptor. (See kinetics of binding).
The units are M-1 sec-1.
k-1
The rate constant for dissociation of a drug from its receptor. (See kinetics of binding).
The units are sec-1.
Kinetics of binding
The simplest assumption about the nature of the binding of drugs to receptors is that one
molecule of drug (D) binds reversibly to one receptor molecule (R) to form a drug-receptor
complex (DR):
k1
D + R <=====> DR
k-1
The rate of the forward reaction is equal to k1[D][R], where k1 is the association rate constant. (The square brackets signify the concentration of the terms they enclose). The rate of the reverse reaction equals k-1[DR], where k-1 is the dissociation rate constant. At equilibrium, the rate of association equals the rate of dissociation, i.e.
k1[D][R] = k-1[DR]
or, rearranging,
k-1 [D][R]
____ = KD = ______
k1 [DR]
KD, the dissociation constant, may thus be defined either as the ratio of the dissociation and association rate constants, or as the concentration of drug which, at equilibrium, occupies 50% of the receptors (i.e. [DR] = [R], so KD = [D]).
Non-specific binding
See NSB.
![]() Competition
assays
Competition
assays
![]() Principles
Principles
![]() Table of Contents
Table of Contents
 |
 |
 |
 |
 |
 |
 |